heap

堆是一种特殊的完全二叉树，有最小堆和最大堆两种。

如图为最小堆，满足所有父结点都比子结点小。最大堆反之。
显然最小堆的特性是根结点的值最小。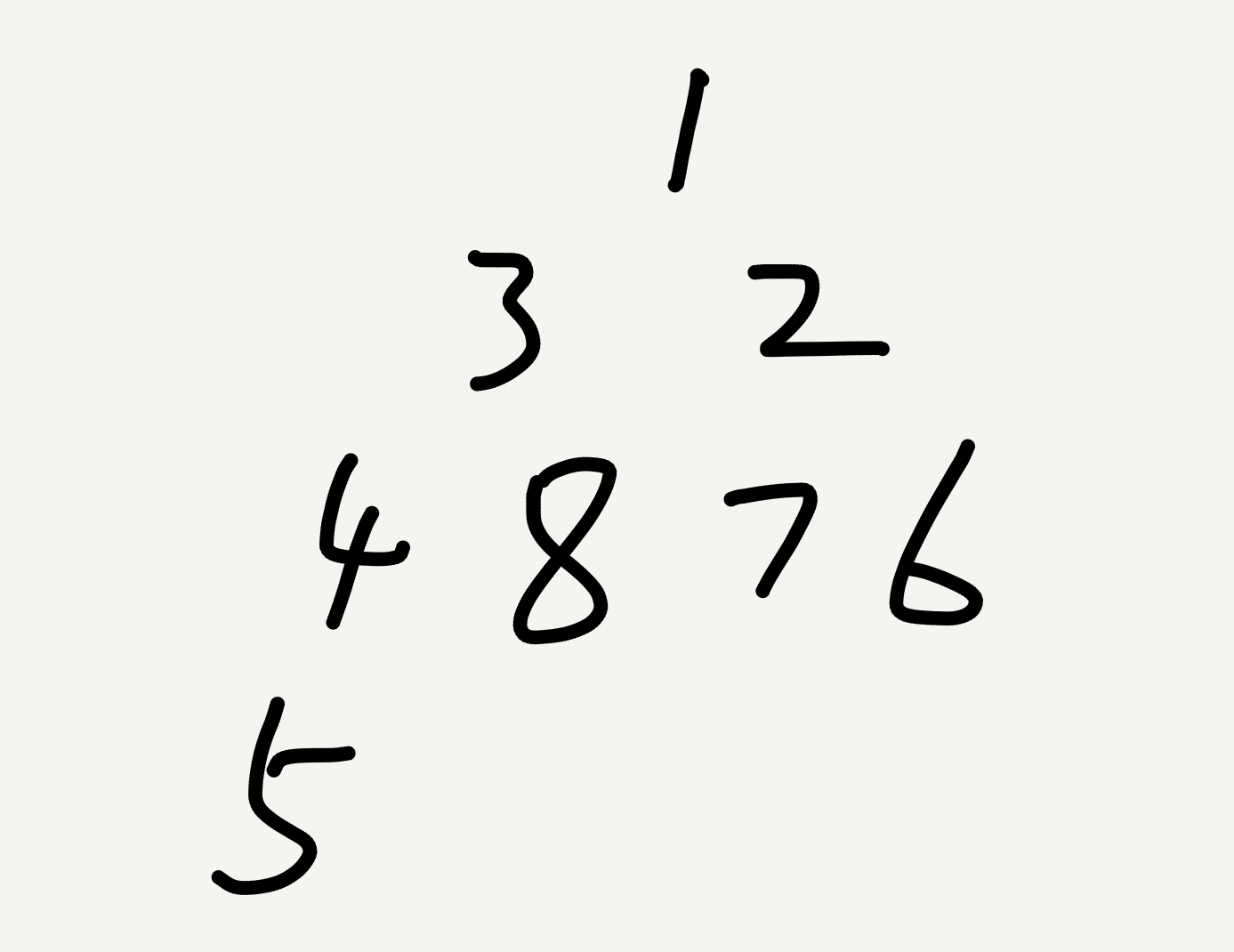

构建最小堆

算法思想
1.把n个元素建立一个堆，注意这里牺牲了h[0]存储，将n个结点自顶向下，从左到右的方式从1到n编码。这样便将n个结点转换为一棵完全二叉树。

1
2
int h[]={0,3,5,6,1,8,7,2,4};
int n=8;    //存储堆中元素个数，即堆的大小

2.从最后一个非叶结点(编号为n/2)开始到根结点(编号为1)逐个扫描，每次扫描就是将结点向下调整。
注：向下调整即让子树符合堆的特性。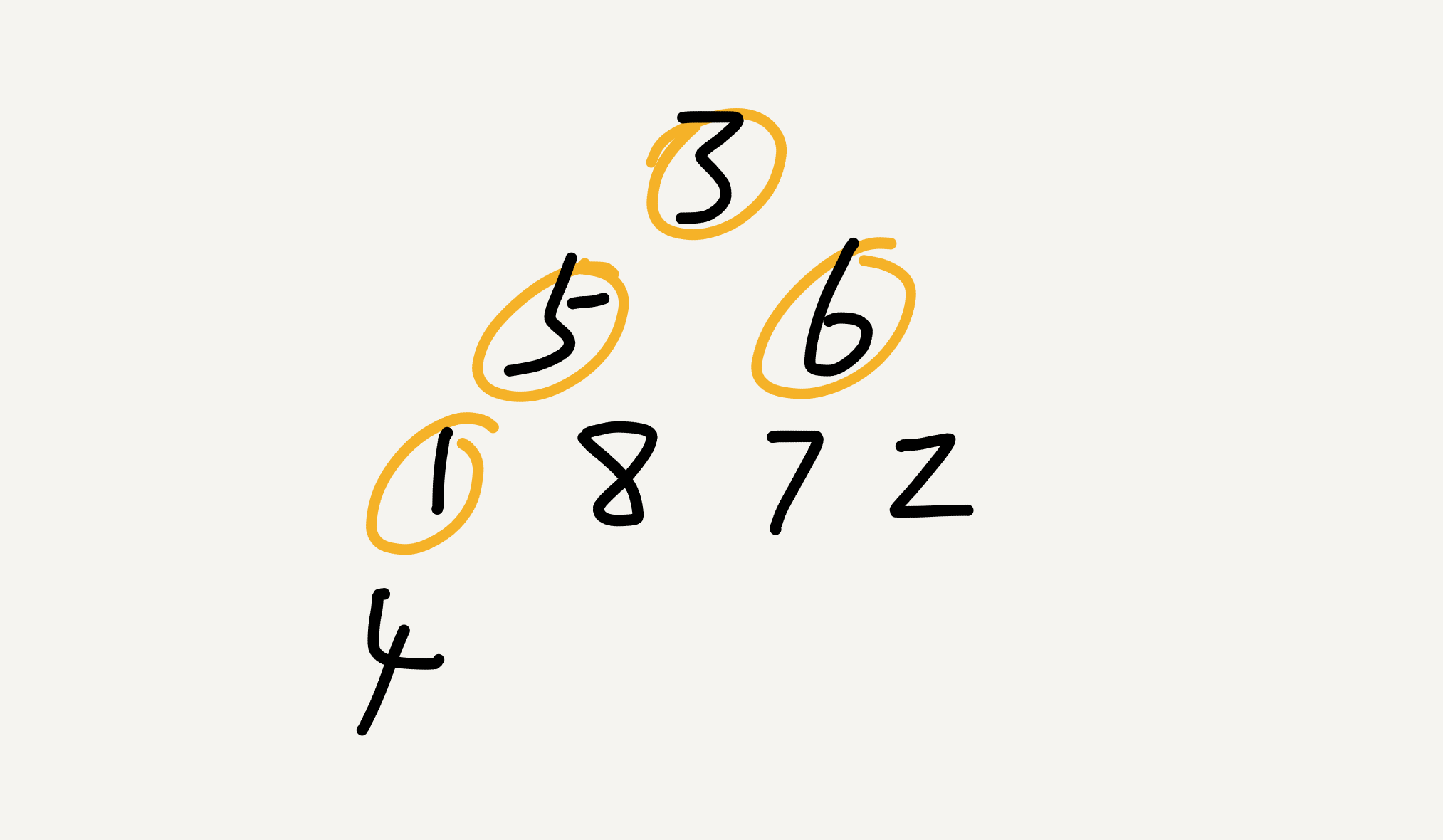

—————————————————代码如下——————————————————

1
2
3
4
5
6
void create()    //构建最小堆 
{
    int i;      //从最后一个非叶结点到第1个结点依次向上调整 
    for(i = n/2; i >= 1; i--)
        siftdown(i);
}

向下调整

从编号为i的结点开始向下调整，因为要构建最小堆，所以要让子树中父结点始终是最小的，如果子结点比父结点小，就交换，继续向上调整。
—————————————————代码如下——————————————————

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void swap(int x, int y)    //交换堆中两个元素的值 
{
    int t;
    t=h[x];
    h[x]=h[y];
    h[y]=t;
}
void siftdown(int i)
{                    //从编号为i的节点开始向下调整 
    int t, flag=0;
    while(i*2 <= n && !flag)//当结点i有儿子并且有需要继续调整的时候就执行 
    {                //t记录值较小的结点编号 
        if(h[i] > h[2*i])    //判断和左儿子的关系 
            t = 2*i;
        else
            t = i;
        if((2*i + 1) <= n)
        {        //如果有右儿子，判断和右儿子关系 
            if(h[t] > h[2*i + 1])
                t = 2*i+1;
        }
        if(t != i)    // t != i，即子结点中有更小的 
        {
            swap(t, i);    //交换两个结点的值
            i=t;        //更新i，继续向下调整 
        }       //反之，不用向下调整了
        else
            flag=1;
    }
}

向上调整

最小堆已经构建好了，如果要插入元素需要向上调整。
从编号为i的非叶结点开始向上调整，为了维护最小堆特性，要将该点与其父结点比较，若父结点较小，就交换，继续向上调整。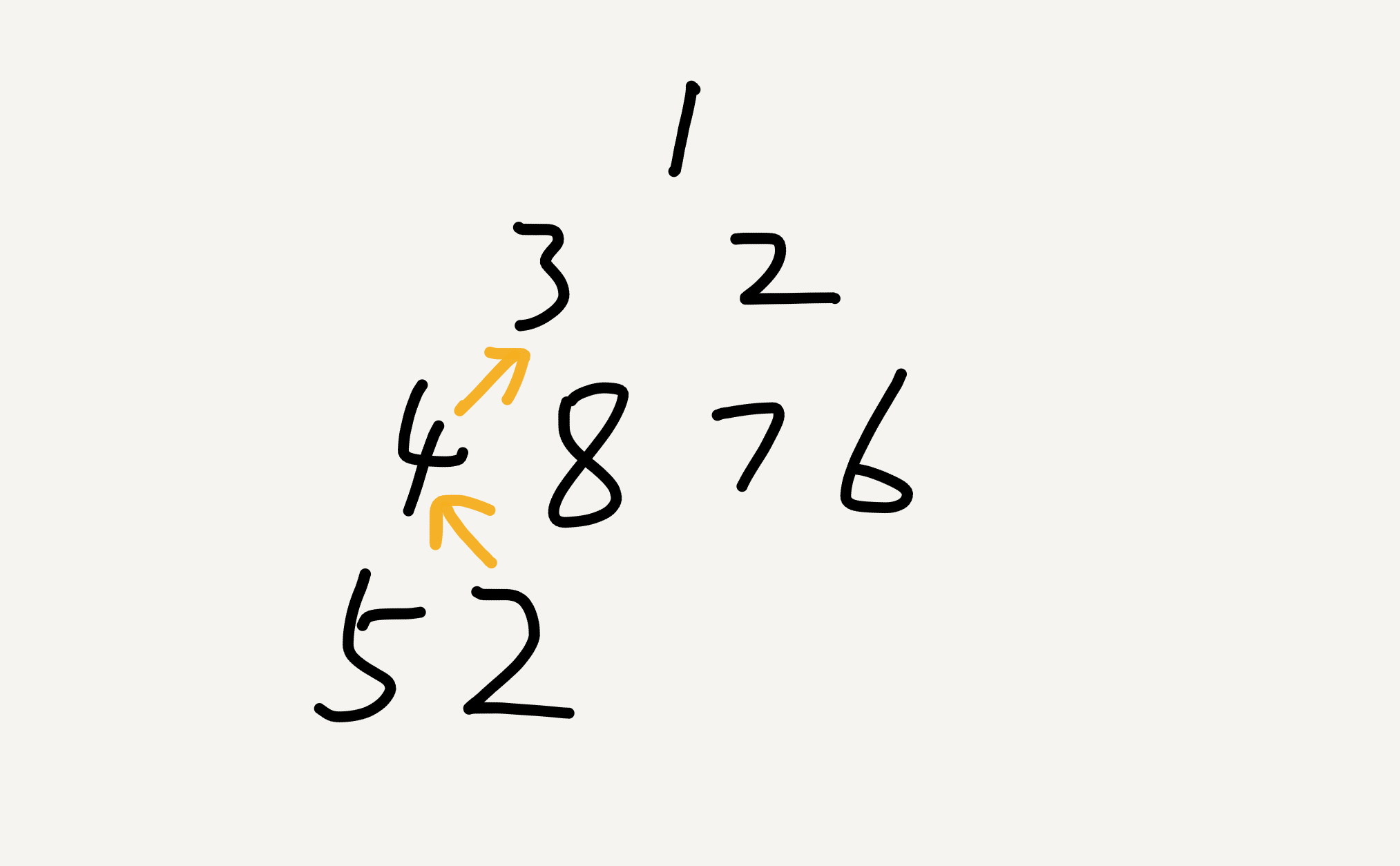

—————————————————代码如下——————————————————

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void siftup(int i)    //从编号为i元素开始向上调整 
{
    int t,flag=0;
    n++;
    while(i!=1 && !flag)
    {           //只需和父结点比较大小即可
        if(h[i]<h[i/2])
            t=i/2;
        else
            t=i;
        if(t!=i)    //如果需要交换，就继续向上调整
        {
            swap(t,i);
            i=t;
        }
        else
            flag=1;
    }
}

堆排序实现

算法思想
1.构建最大堆，这样最大的元素在h[1]，然后将h[1]与h[n]交换(最大的已归位)，记得h[1]向下调整以保持堆的特性。
2.执行–n，h[1]与h[n]交换(第二大的已归为)，h[1]向下调整。如此反复，直到堆的大小为1。

堆排序的时间复杂度O(n log n)
—————————————————代码如下——————————————————

1
2
3
4
5
6
7
8
9
void heapsort()  //堆排序 
{
    while(n>1)   //将h[1]和h[n]交换得到最大元素h[n],然后将h[1]向下调整 
    {
        swap(1,n);
        n--;     //直到堆的大小为1为止 
        siftdown(1);
    }
}