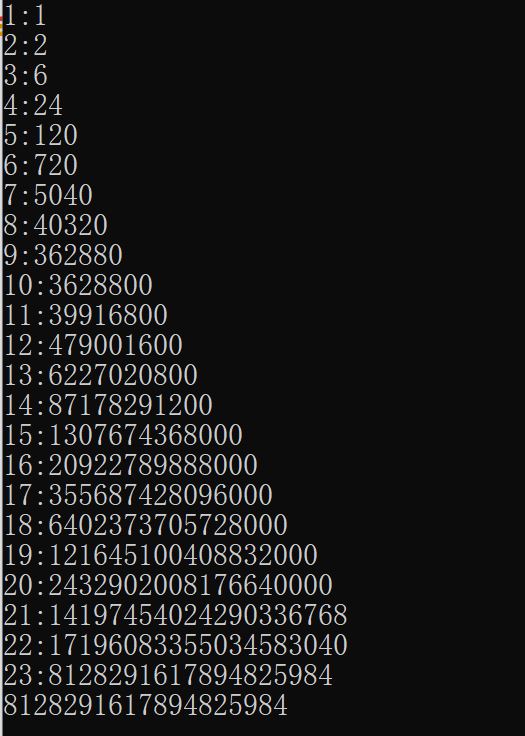
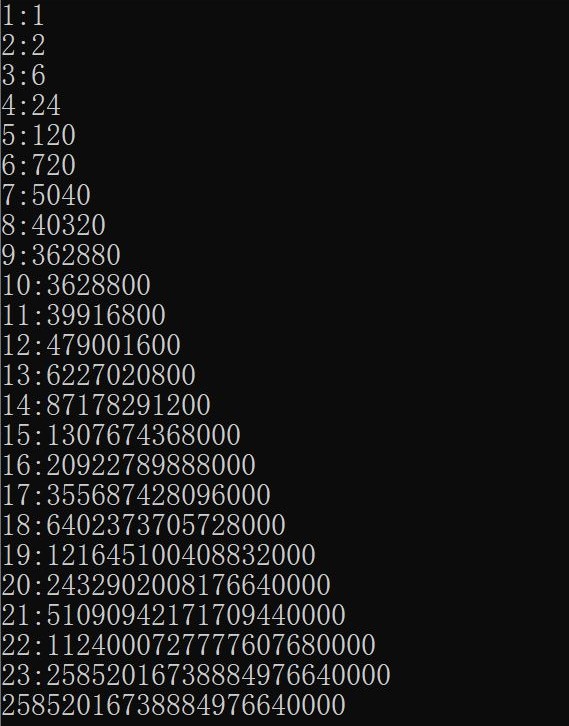
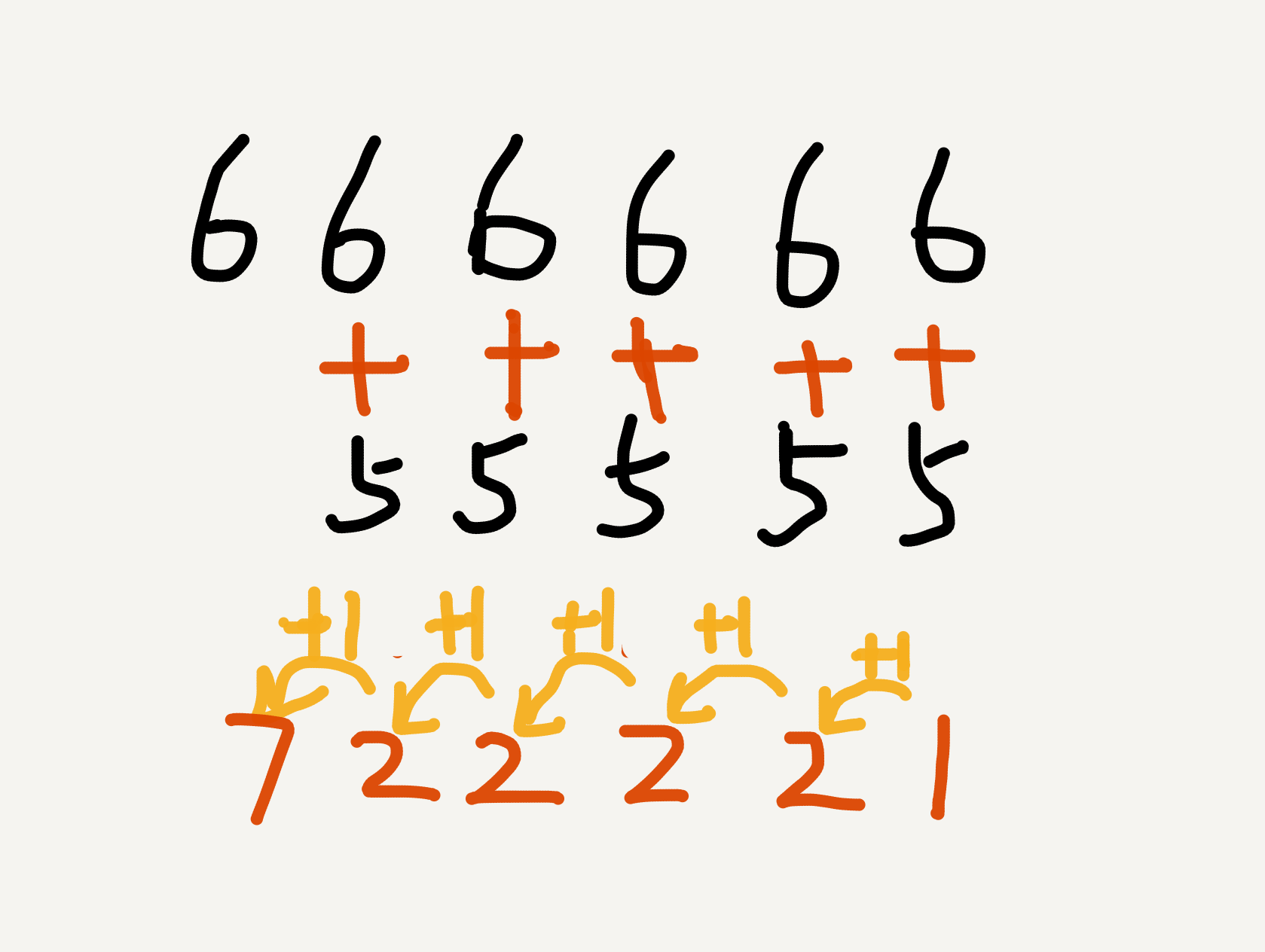n的阶乘求f(n)递归实现只能算到n = 20, 再想计算显然用高精度乘法(字符串存储)可以实现。
————————————n=23运行结果(左图递归、右图高精度)———————————————
算法思想
f(n) = 1* 2* 3…n
其中 f(i)*f(i+1) 使用高精度乘法,那么调用n-1次即可
这里使用高精度加法实现高精度乘法,所以先介绍高精度加法
高精度加法其实就是计算两个数相加的过程,使用多个存储单元,将数字字符存储到串中,就可以实现数值范围较大的加法运算,如图。
$ 666666+55555=(6+5)+(60+50)+(600+500)+(6000+5000)+(600000+50000)+(600000) $
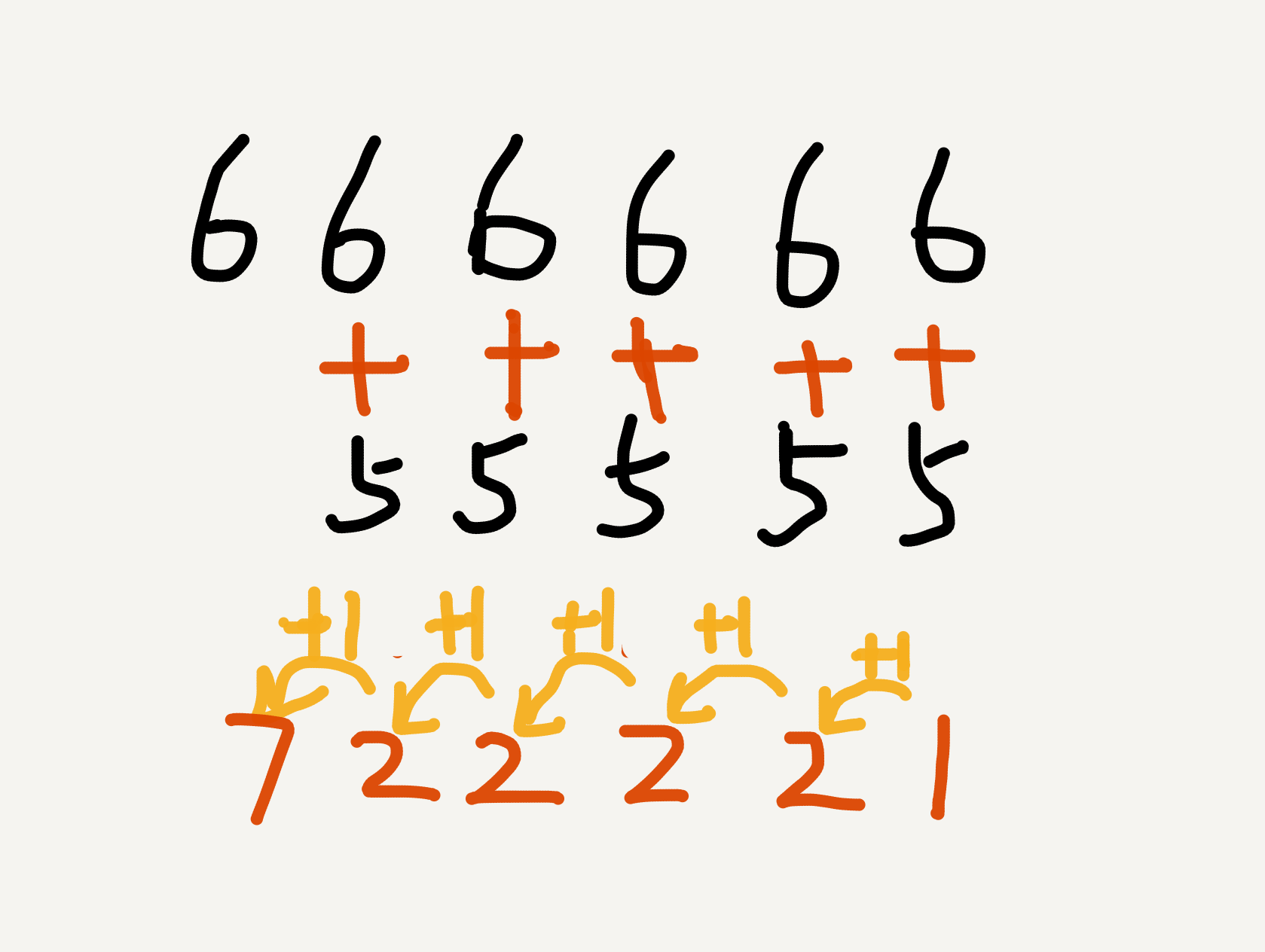
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| string Add(string a, string b)
{
string sum;
if(a.size() < b.size())
{
string temp;
temp = a;
a = b;
b = temp;
}
int len = a.size();
a = '0'+a;
for(int i=len-b.size(); i>=0; --i)
b = '0'+b;
for(int i=0; i<=len; ++i)
sum += '0';
int t,c=0;
for(int i=len; i>=0; --i)
{
t = ((a[i]-'0')+(b[i]-'0')+c);
c = t/10;
sum[i] += t%10;
}
if(sum[0]=='0')
sum = sum.substr(1, sum.size());
return sum;
}
|
乘法其实就是多次相加,所以高精度乘法可以由多次高精度加法实现 a*b 即 b个a相加, 如图
$ 333333\times22222 = 333333\times\left(20000+2000+200+20+2\right) $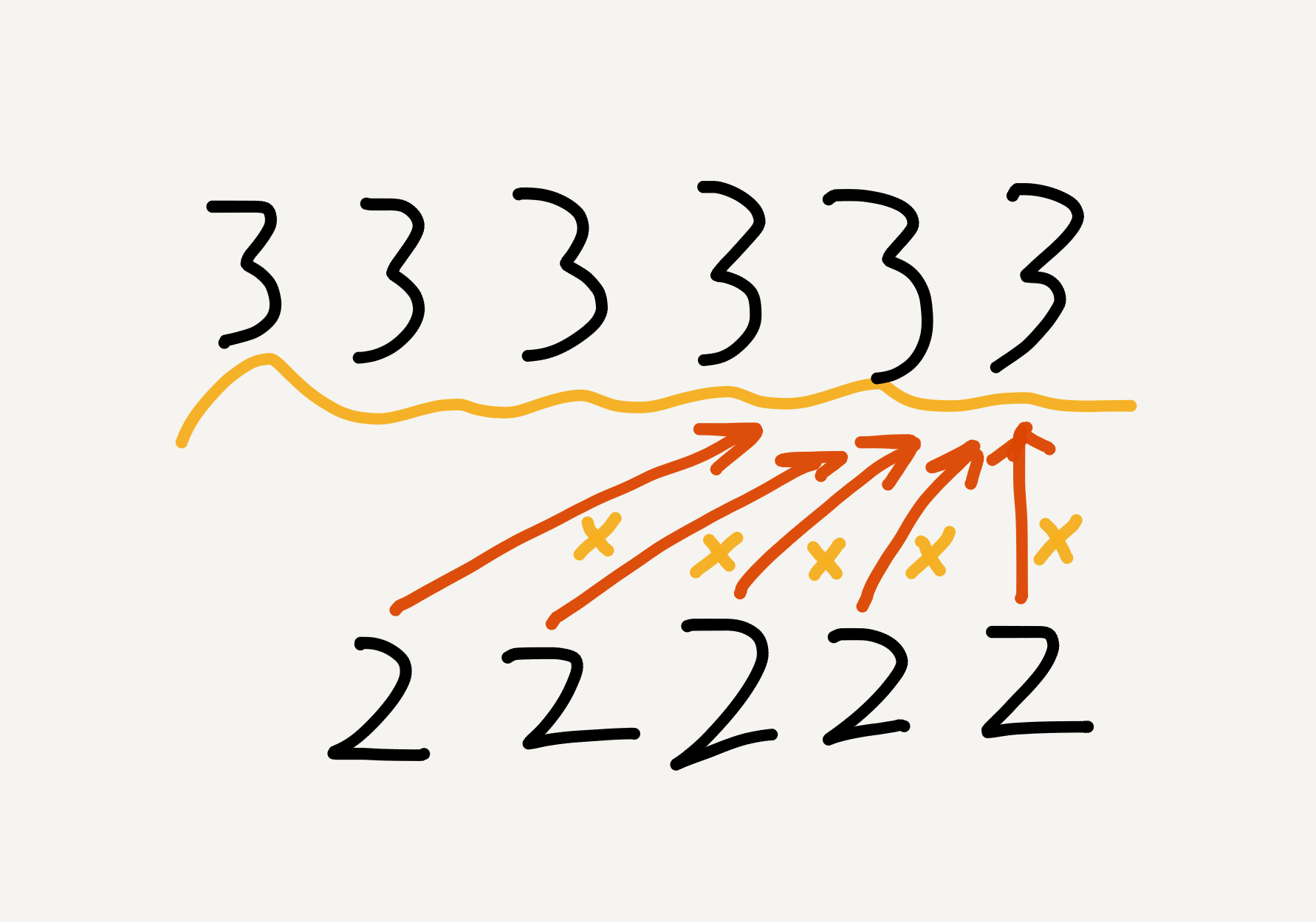
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| string Mult(string a, string b)
{
if(a.size()<b.size())
{
string temp;
temp = a;
a = b;
b = temp;
}
int len=b.size();
string sum="0";
for(int i=len-1; i>=0; --i)
{
if(i<len-1)
a += '0';
string ans = a;
if(b[i] != '0')
{
for(int j=1; j<b[i]-'0'; ++j)
ans = Add(ans, a);
sum = Add(sum, ans);
}
}
return sum;
}
|
接着计算n的阶乘就很容易了
1
2
3
4
5
6
7
8
9
10
| string Sum(int n)
{
string sum = "1";
int i = 1;
while(n > i)
{
sum = Mult(sum, to_string(++i));
}
return sum;
}
|