归并（Merge）排序法，即把待排序序列分为若干个子序列，每个子序列是有序的，然后再把有序子序列合并为整体有序序列。

算法分析
每一趟归并的时间复杂度为O(n)，共需要进行log2n趟。对应的算法的时间复杂度为O(nlog2n)

例：
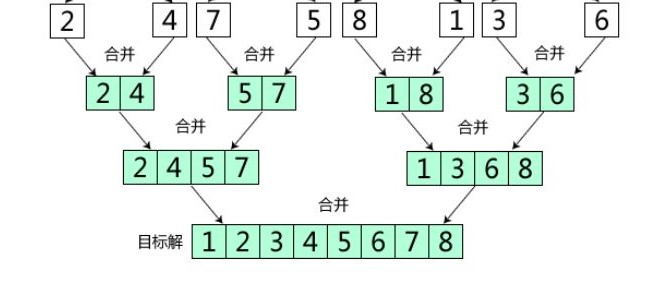
Input 2 4 7 5 8 1 3 6
Output 1 2 3 4 5 6 7 8

递归实现归并算法

• 算法思想
  将待排元素分成大小大致相同的两个子集，分别对两个子集合排序，最终将排好序的子集合合并
  设归并排序的当前区间为R[low…high],分治法的三个步骤：
  1、分解 当前区间一分为二
  2、求解 递归对两个子区间R[low…mid]和R[mid+1…high]
  3、组合 将已排序的两个子区间R[low…mid]和R[mid+1…high]合并为一个有序区间R[low…high]
  递归终止条件：子区间长度为1
  

Mergesort函数实现步骤1、2

void mergesort(int a[], int low, int high)
{
	int middle = (low + high)/2;
	if(low<high)
	{
		mergesort(a, low, middle);
		mergesort(a, middle+1, high);
		sort(a, low, middle, high);
		cout<<" low: "<<low<<" middle: "<<middle<<" high: "<<high<<endl;

	}
}

Sort函数实现步骤3

void sort(int a[], int low, int middle, int high)
{
	int i = low, j = middle+1, k = 0;
	int *b= new int[high-low+1];
	while(i<=middle && j<=high)
	{
		if(a[i] <= a[j])
			b[k++] = a[i++];
		else
			b[k++] = a[j++];
	}
	while(i<=middle)
		b[k++] = a[i++];
	while(j<=high)
		b[k++] = a[j++];
	for(k=0,i=low; i<=high; k++,i++)
		a[i] = b[k];
	delete []b;
}

————————完整代码————————

#include <iostream>
#include <cstdlib>
#include <new> 
using namespace std;

void sort(int a[], int low, int middle, int high)
{
	int i = low, j = middle+1, k = 0;
	int *b= new int[high-low+1];
	while(i<=middle && j<=high)
	{
		if(a[i] <= a[j])
			b[k++] = a[i++];
		else
			b[k++] = a[j++];
	}
	while(i<=middle)
		b[k++] = a[i++];
	while(j<=high)
		b[k++] = a[j++];
	for(k=0,i=low; i<=high; k++,i++)
		a[i] = b[k];
	delete []b;
}
void mergesort(int a[], int low, int high)
{
	int middle = (low + high)/2;
	if(low<high)
	{
		mergesort(a, low, middle);
		mergesort(a, middle+1, high);
		sort(a, low, middle, high);
		cout<<" low: "<<low<<" middle: "<<middle<<" high: "<<high<<endl;

	}
}
int main()
{
	int a[] = {2, 4, 7, 5, 8, 1, 3, 6};
	mergesort(a, 0, 7);
	for(int i=0; i<8; i++)
		printf("%d ", a[i]);
	printf("\n");
	return 0;
}

非递归实现归并算法

• 算法思想
  将数组中的相邻元素两两配对，构成((length-1)/2+1)组排序好的子数组段，然后在合并（(length-1）/4+1)组子数组段，直到整个数组排序好

与递归实现相比仅mergesort函数不同
主函数调用时改为

mergesort(a, 8);

void mergesort(int a[], int length)
{
	int low, middle, high, size = 1;
	while(size < length-1)
	{
		low = 0;
		while(low+size < length-1)
		{
			middle = low+size-1;
			high = middle+size;
			if(high>length-1)
				high = length-1;
			sort(a, low, middle, high);
			cout<<" low: "<<low<<" middle: "<<middle<<" high: "<<high<<endl;
			low = high+1;
		}
		size *= 2;
	}
}

自然排序实现归并算法

• 算法思想
  对于初始数组a，通常存在多个长度大于1的已排好序的子数组段，找出这样的子数组段，然后将相邻的排好序的子数组段两两合并，直至整个数组排好序

1.Mergepass函数实时查询数组a中有多少组排好序的子数组
2.将返回值传给Mergesort函数，再进行有序子序列的合并
3.合并操作调用Sort函数

完整代码

#include <iostream>
#include <cstdlib>
#include <new> 
#include <cstring>
using namespace std;

int s[100]; 
void Sort(int a[], int low, int middle, int high)
{
	int i = low, j = middle+1, k = 0;
	int *b= new int[high-low+1];
	while(i<=middle && j<=high)
	{
		if(a[i] <= a[j])
			b[k++] = a[i++];
		else
			b[k++] = a[j++];
	}
	while(i<=middle)
		b[k++] = a[i++];
	while(j<=high)
		b[k++] = a[j++];
	for(k=0,i=low; i<=high; k++,i++)
		a[i] = b[k];
	delete []b;
}
int Mergepass(int x[], int n)
{
	int k=0;
	int begin = x[0];
	s[k++] = 0;
	for(int i=1; i<n; i++)
	{
		if(x[i] < begin)
			s[k++] = i;
		begin = x[i];
	}
	s[k++] = n;
	return k;
}
void Mergesort(int a[], int length)
{
	int Num = Mergepass(a, length);//返回的是子数组段个数+1
	while(Num != 2)
	{
		for(int i=0; i+1<Num; i+=2)
			Sort(a, s[i], s[i+1]-1, s[i+2]-1);
		//即递归实现合并中的Sort(a,low,middle,high)
		Num = Mergepass(a, length);
	}
}

int  main()
{ 
  	int num[] = {2, 4, 7, 5, 8, 1, 3, 6};    
    Mergesort(num,8);   
    for(int i=0;i<8;i++)
    	cout<<num[i]<<' ';  
	cout<<endl;    
    return 0;       
}